4 - Evaluating models

Survival analysis with tidymodels

Predictions

For our demo data set of n = 50 cats, we’ll make predictions every 30 days for roughly the first 10 months:

demo_cat_preds <- augment(tree_fit, demo_cats, eval_time = ((1:10) * 30))
demo_cat_preds |> select(1:3)
#> # A tibble: 50 × 3
#>    .pred             .pred_time event_time
#>    <list>                 <dbl>     <Surv>
#>  1 <tibble [10 × 5]>      1.08         36 
#>  2 <tibble [10 × 5]>      0.594        16+
#>  3 <tibble [10 × 5]>      0.594        12+
#>  4 <tibble [10 × 5]>      1.08         16 
#>  5 <tibble [10 × 5]>      2.39         22 
#>  6 <tibble [10 × 5]>      0.594        16 
#>  7 <tibble [10 × 5]>      1.08        294 
#>  8 <tibble [10 × 5]>      0.594        68+
#>  9 <tibble [10 × 5]>      1.08         31 
#> 10 <tibble [10 × 5]>      0.594        24+
#> # ℹ 40 more rows

Concordance

The concordance statistic (“c-index”, Harrell et al (1996)) is a metric that quantifies that the rank order of the times is consistent with the model score.

It takes into account censoring and does not depend on a specific evaluation time. The range of values is \([-1, 1]\).

demo_cat_preds |> 
  concordance_survival(event_time, estimate = .pred_time)
#> # A tibble: 1 × 3
#>   .metric              .estimator .estimate
#>   <chr>                <chr>          <dbl>
#> 1 concordance_survival standard       0.312

Time-dependent metrics

Classification(ish) metrics

Most dynamic metrics convert the survival probabilities to events and non-events based on some probability threshold.

From there, we can apply existing classification metrics, such as

  • Brier Score (for calibration)
  • Area under the ROC curve (for separation)

More details on dynamics metrics at tidymodels.org

Converting to events

Converting to events

For a specific evaluation time point \(\tau\), we convert the observed event time to a binary event/non-event version, if possible.

\[ y_{i\tau} = \begin{cases} 0 & \text{if } \tau \lt t_{i} \text{ and } either \notag \\ 1 & \text{if } \tau \geq t_{i} \text{ and event} \notag \\ missing & \text{if } \tau \geq t_{i} \text{ and censored } \end{cases} \]

Dealing with missing outcome data

Without censored data points, this conversion would yield appropriate performance estimates since no event outcomes would be missing.


Otherwise, there is the potential for bias due to missingness.


We’ll use tools from causal inference to compensate by creating a propensity score that uses the probability of being censored/missing.

Case weights use the inverse of this probability. See Graf et al (1999).

Brier score

The Brier score is calibration metric originally meant for classification models:

\[ Brier = \frac{1}{N}\sum_{i=1}^N\sum_{k=1}^C (y_{ik} - \hat{\pi}_{ik})^2 \]

Brier score

For our application, we have two classes and case weights \(w_{it}\)

\[ Brier(t) = \frac{1}{N}\sum_{i=1}^N w_{it} \left[ \begin{aligned} &\underbrace{I(y_{it} = 0)((1 - y_{it}) - \hat{p}_{it})^2}_\text{non-events} \\ &+ \underbrace{I(y_{it} = 1)(y_{it} - (1 - \hat{p}_{it}))^2}_\text{events} \end{aligned} \right] \]

where \(N\) is the number of non-missing rows in the data.

Brier scores

demo_brier <- brier_survival(demo_cat_preds, truth = event_time, .pred)
demo_brier
#> # A tibble: 10 × 4
#>    .metric        .estimator .eval_time .estimate
#>    <chr>          <chr>           <dbl>     <dbl>
#>  1 brier_survival standard           30     0.151
#>  2 brier_survival standard           60     0.174
#>  3 brier_survival standard           90     0.148
#>  4 brier_survival standard          120     0.170
#>  5 brier_survival standard          150     0.159
#>  6 brier_survival standard          180     0.185
#>  7 brier_survival standard          210     0.147
#>  8 brier_survival standard          240     0.156
#>  9 brier_survival standard          270     0.162
#> 10 brier_survival standard          300     0.129

Brier scores over evaluation time

Integrated Brier Score

brier_survival_integrated(demo_cat_preds, truth = event_time, .pred)
#> # A tibble: 1 × 3
#>   .metric                   .estimator .estimate
#>   <chr>                     <chr>          <dbl>
#> 1 brier_survival_integrated standard       0.144

Area Under the ROC Curve

We can use the standard ROC curve machinery on the indicators, probabilities, and censoring weights at evaluation time \(\tau\).
See Hung and Chiang (2010).


ROC curves measure the separation between events and non-events and are ignorant of how well-calibrated the probabilities are.

Area under the ROC curve

demo_roc_auc <- roc_auc_survival(demo_cat_preds, truth = event_time, .pred)
demo_roc_auc
#> # A tibble: 10 × 4
#>    .metric          .estimator .eval_time .estimate
#>    <chr>            <chr>           <dbl>     <dbl>
#>  1 roc_auc_survival standard           30     0.704
#>  2 roc_auc_survival standard           60     0.615
#>  3 roc_auc_survival standard           90     0.556
#>  4 roc_auc_survival standard          120     0.556
#>  5 roc_auc_survival standard          150     0.552
#>  6 roc_auc_survival standard          180     0.552
#>  7 roc_auc_survival standard          210     0.481
#>  8 roc_auc_survival standard          240     0.481
#>  9 roc_auc_survival standard          270     0.481
#> 10 roc_auc_survival standard          300     0.483

ROC AUC over evaluation time

Setting evaluation times

  • You can get predictions at any values of \(\tau\).
  • During model development, we suggest picking a more focused set of evaluation times (for computational time).
  • You should also pick a single time to perform your optimizations/comparisons with and list that value first in the vector. If 90 days was of particular interest over a 30-to-120-day span, you’d use
eval_times <- c(90, 30, 60, 120)

⚠️ DANGERS OF OVERFITTING ⚠️

Your turn

Why haven’t we done this?

tree_fit |>
  augment(cat_train, eval_time = ((1:10) * 30)) |>
  brier_survival(truth = event_time, .pred)
05:00

The testing data are precious 💎

How can we use the training data to compare and evaluate different models? 🤔

Cross-validation 

set.seed(123)
cat_folds <- vfold_cv(cat_train, v = 10) # v = 10 is default
cat_folds
#> #  10-fold cross-validation 
#> # A tibble: 10 × 2
#>    splits             id    
#>    <list>             <chr> 
#>  1 <split [1588/177]> Fold01
#>  2 <split [1588/177]> Fold02
#>  3 <split [1588/177]> Fold03
#>  4 <split [1588/177]> Fold04
#>  5 <split [1588/177]> Fold05
#>  6 <split [1589/176]> Fold06
#>  7 <split [1589/176]> Fold07
#>  8 <split [1589/176]> Fold08
#>  9 <split [1589/176]> Fold09
#> 10 <split [1589/176]> Fold10

Cross-validation

What is in this?

cat_folds$splits[1:3]
#> [[1]]
#> <Analysis/Assess/Total>
#> <1588/177/1765>
#> 
#> [[2]]
#> <Analysis/Assess/Total>
#> <1588/177/1765>
#> 
#> [[3]]
#> <Analysis/Assess/Total>
#> <1588/177/1765>

Set the seed when creating resamples

Bootstrapping 

set.seed(3214)
bootstraps(cat_train)
#> # Bootstrap sampling 
#> # A tibble: 25 × 2
#>    splits             id         
#>    <list>             <chr>      
#>  1 <split [1765/657]> Bootstrap01
#>  2 <split [1765/644]> Bootstrap02
#>  3 <split [1765/625]> Bootstrap03
#>  4 <split [1765/638]> Bootstrap04
#>  5 <split [1765/647]> Bootstrap05
#>  6 <split [1765/655]> Bootstrap06
#>  7 <split [1765/655]> Bootstrap07
#>  8 <split [1765/637]> Bootstrap08
#>  9 <split [1765/669]> Bootstrap09
#> 10 <split [1765/638]> Bootstrap10
#> # ℹ 15 more rows

The whole game - status update

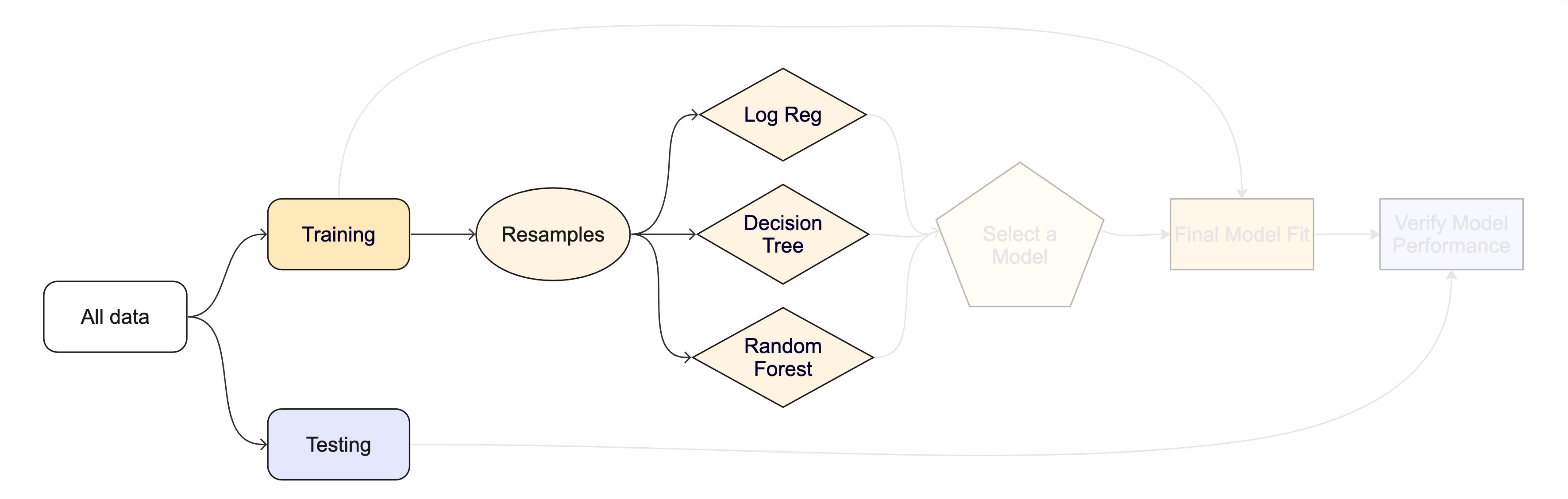
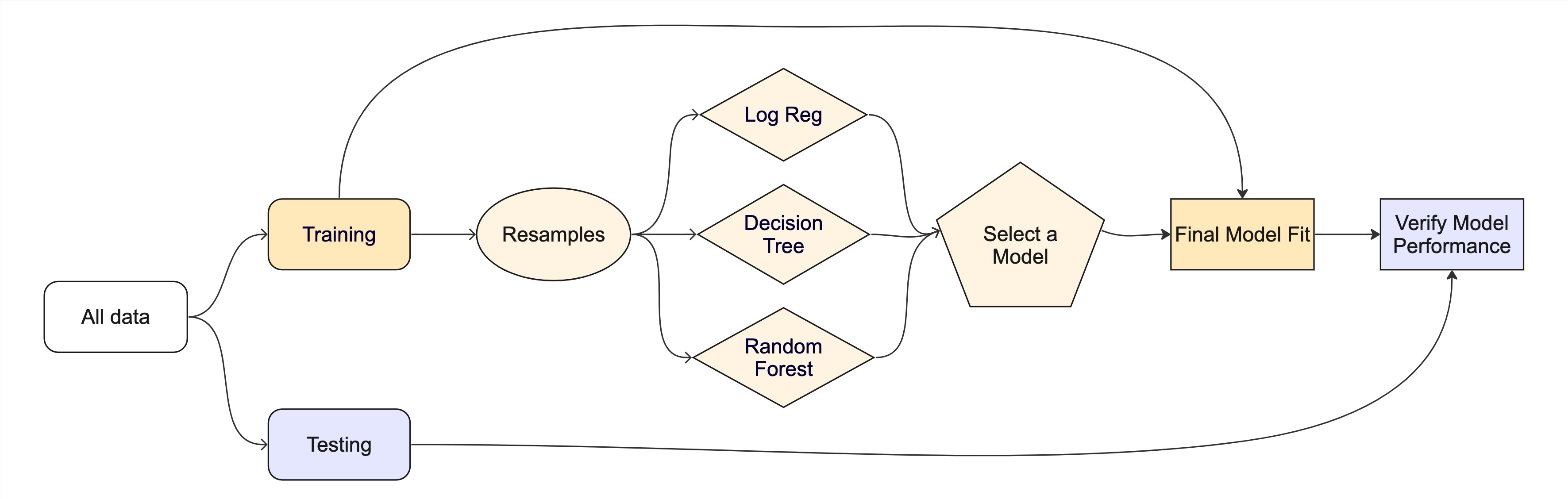
We are equipped with metrics and resamples!

Fit our model to the resamples

tree_wflow <- workflow(event_time ~ ., tree_spec)

tree_res <- fit_resamples(tree_wflow, cat_folds, eval_time = c(90, 30, 60, 120))
tree_res
#> # Resampling results
#> # 10-fold cross-validation 
#> # A tibble: 10 × 4
#>    splits             id     .metrics         .notes          
#>    <list>             <chr>  <list>           <list>          
#>  1 <split [1588/177]> Fold01 <tibble [4 × 5]> <tibble [0 × 3]>
#>  2 <split [1588/177]> Fold02 <tibble [4 × 5]> <tibble [0 × 3]>
#>  3 <split [1588/177]> Fold03 <tibble [4 × 5]> <tibble [0 × 3]>
#>  4 <split [1588/177]> Fold04 <tibble [4 × 5]> <tibble [0 × 3]>
#>  5 <split [1588/177]> Fold05 <tibble [4 × 5]> <tibble [0 × 3]>
#>  6 <split [1589/176]> Fold06 <tibble [4 × 5]> <tibble [0 × 3]>
#>  7 <split [1589/176]> Fold07 <tibble [4 × 5]> <tibble [0 × 3]>
#>  8 <split [1589/176]> Fold08 <tibble [4 × 5]> <tibble [0 × 3]>
#>  9 <split [1589/176]> Fold09 <tibble [4 × 5]> <tibble [0 × 3]>
#> 10 <split [1589/176]> Fold10 <tibble [4 × 5]> <tibble [0 × 3]>

Evaluating model performance 

tree_res |>
  collect_metrics()
#> # A tibble: 4 × 7
#>   .metric        .estimator .eval_time  mean     n std_err .config             
#>   <chr>          <chr>           <dbl> <dbl> <int>   <dbl> <chr>               
#> 1 brier_survival standard           30 0.266    10 0.00498 Preprocessor1_Model1
#> 2 brier_survival standard           60 0.264    10 0.00952 Preprocessor1_Model1
#> 3 brier_survival standard           90 0.330    10 0.00599 Preprocessor1_Model1
#> 4 brier_survival standard          120 0.155    10 0.00978 Preprocessor1_Model1

We can reliably measure performance using only the training data 🎉

Where are the fitted models? 

tree_res
#> # Resampling results
#> # 10-fold cross-validation 
#> # A tibble: 10 × 4
#>    splits             id     .metrics         .notes          
#>    <list>             <chr>  <list>           <list>          
#>  1 <split [1588/177]> Fold01 <tibble [4 × 5]> <tibble [0 × 3]>
#>  2 <split [1588/177]> Fold02 <tibble [4 × 5]> <tibble [0 × 3]>
#>  3 <split [1588/177]> Fold03 <tibble [4 × 5]> <tibble [0 × 3]>
#>  4 <split [1588/177]> Fold04 <tibble [4 × 5]> <tibble [0 × 3]>
#>  5 <split [1588/177]> Fold05 <tibble [4 × 5]> <tibble [0 × 3]>
#>  6 <split [1589/176]> Fold06 <tibble [4 × 5]> <tibble [0 × 3]>
#>  7 <split [1589/176]> Fold07 <tibble [4 × 5]> <tibble [0 × 3]>
#>  8 <split [1589/176]> Fold08 <tibble [4 × 5]> <tibble [0 × 3]>
#>  9 <split [1589/176]> Fold09 <tibble [4 × 5]> <tibble [0 × 3]>
#> 10 <split [1589/176]> Fold10 <tibble [4 × 5]> <tibble [0 × 3]>

🗑️

But it’s easy to save the predictions 

# Save the assessment set results
ctrl_cat <- control_resamples(save_pred = TRUE)
tree_res <- fit_resamples(tree_wflow, cat_folds, eval_time = c(90, 30, 60, 120),
                          control = ctrl_cat)

tree_res
#> # Resampling results
#> # 10-fold cross-validation 
#> # A tibble: 10 × 5
#>    splits             id     .metrics         .notes           .predictions
#>    <list>             <chr>  <list>           <list>           <list>      
#>  1 <split [1588/177]> Fold01 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  2 <split [1588/177]> Fold02 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  3 <split [1588/177]> Fold03 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  4 <split [1588/177]> Fold04 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  5 <split [1588/177]> Fold05 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  6 <split [1589/176]> Fold06 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  7 <split [1589/176]> Fold07 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  8 <split [1589/176]> Fold08 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#>  9 <split [1589/176]> Fold09 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>    
#> 10 <split [1589/176]> Fold10 <tibble [4 × 5]> <tibble [0 × 3]> <tibble>

But it’s easy to collect the predictions 

tree_preds <- collect_predictions(tree_res)
tree_preds
#> # A tibble: 1,765 × 5
#>    .pred            id      .row event_time .config             
#>    <list>           <chr>  <int>     <Surv> <chr>               
#>  1 <tibble [4 × 3]> Fold01    17        35  Preprocessor1_Model1
#>  2 <tibble [4 × 3]> Fold01    29        60  Preprocessor1_Model1
#>  3 <tibble [4 × 3]> Fold01    51         8  Preprocessor1_Model1
#>  4 <tibble [4 × 3]> Fold01    55        39+ Preprocessor1_Model1
#>  5 <tibble [4 × 3]> Fold01    62        36+ Preprocessor1_Model1
#>  6 <tibble [4 × 3]> Fold01    63        14  Preprocessor1_Model1
#>  7 <tibble [4 × 3]> Fold01    92        14+ Preprocessor1_Model1
#>  8 <tibble [4 × 3]> Fold01    95        37  Preprocessor1_Model1
#>  9 <tibble [4 × 3]> Fold01    96        19+ Preprocessor1_Model1
#> 10 <tibble [4 × 3]> Fold01   101        83  Preprocessor1_Model1
#> # ℹ 1,755 more rows

Decision tree 🌳

Random forest 🌳🌲🌴🌵🌴🌳🌳🌴🌲🌵🌴🌲🌳🌴🌳🌵🌵🌴🌲🌲🌳🌴🌳🌴🌲🌴🌵🌴🌲🌴🌵🌲🌵🌴🌲🌳🌴🌵🌳🌴🌳

Random forest 🌳🌲🌴🌵🌳🌳🌴🌲🌵🌴🌳🌵

  • Ensemble many decision tree models

  • All the trees vote! 🗳️

  • Bootstrap aggregating + random predictor sampling

  • Often works well without tuning hyperparameters (more on this in a moment), as long as there are enough trees

Create a random forest model 

rf_spec <- rand_forest(trees = 1000) |> 
  set_engine("aorsf") |> 
  set_mode("censored regression")
rf_spec
#> Random Forest Model Specification (censored regression)
#> 
#> Main Arguments:
#>   trees = 1000
#> 
#> Computational engine: aorsf

Create a random forest model 

rf_wflow <- workflow(event_time ~ ., rf_spec)
rf_wflow
#> ══ Workflow ══════════════════════════════════════════════════════════
#> Preprocessor: Formula
#> Model: rand_forest()
#> 
#> ── Preprocessor ──────────────────────────────────────────────────────
#> event_time ~ .
#> 
#> ── Model ─────────────────────────────────────────────────────────────
#> Random Forest Model Specification (censored regression)
#> 
#> Main Arguments:
#>   trees = 1000
#> 
#> Computational engine: aorsf

Your turn

Use fit_resamples() and rf_wflow to:

  • keep predictions
  • compute metrics
08:00

Evaluating model performance 

ctrl_cat <- control_resamples(save_pred = TRUE)

# Random forest uses random numbers so set the seed first
set.seed(2)
rf_res <- fit_resamples(rf_wflow, cat_folds, eval_time = c(90, 30, 60, 120), 
                        control = ctrl_cat)

collect_metrics(rf_res)
#> # A tibble: 4 × 7
#>   .metric        .estimator .eval_time  mean     n std_err .config             
#>   <chr>          <chr>           <dbl> <dbl> <int>   <dbl> <chr>               
#> 1 brier_survival standard           30 0.210    10 0.00455 Preprocessor1_Model1
#> 2 brier_survival standard           60 0.241    10 0.00796 Preprocessor1_Model1
#> 3 brier_survival standard           90 0.199    10 0.00960 Preprocessor1_Model1
#> 4 brier_survival standard          120 0.151    10 0.00840 Preprocessor1_Model1

The whole game - status update

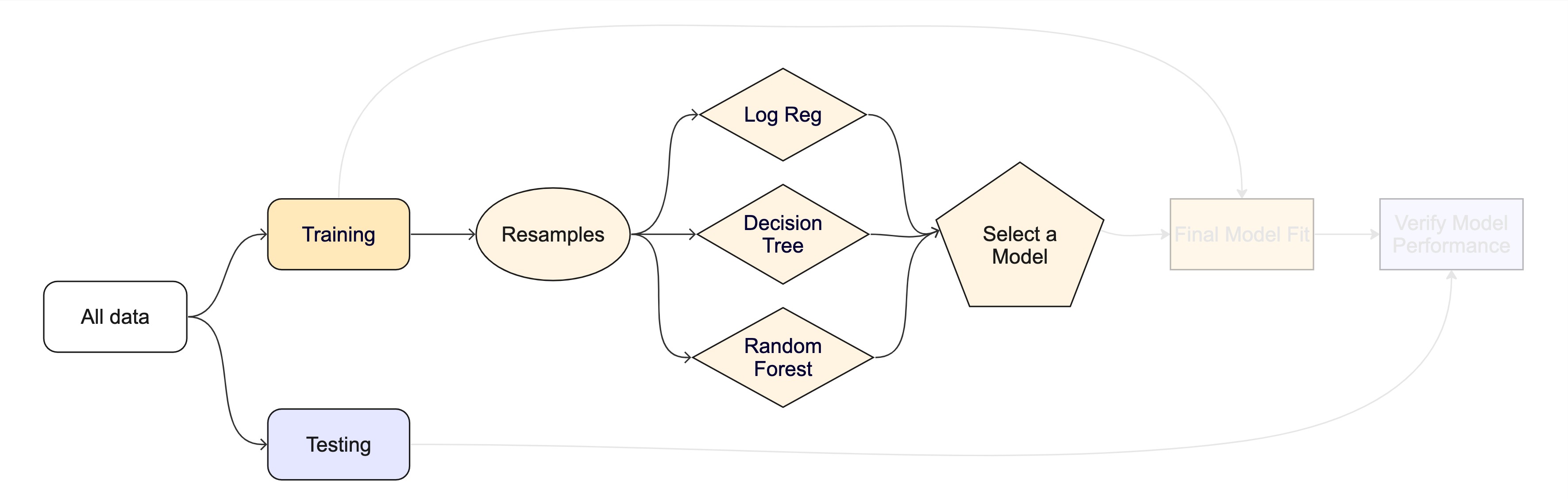
The final fit

Suppose that we are happy with our random forest model.

Let’s fit the model on the training set and verify our performance using the test set.

We’ve shown you fit() and predict() (+ augment()) but there is a shortcut:

# cat_split has train + test info
final_fit <- last_fit(rf_wflow, cat_split, eval_time = c(90, 30, 60, 120)) 

final_fit
#> # Resampling results
#> # Manual resampling 
#> # A tibble: 1 × 6
#>   splits             id               .metrics .notes   .predictions .workflow 
#>   <list>             <chr>            <list>   <list>   <list>       <list>    
#> 1 <split [1765/442]> train/test split <tibble> <tibble> <tibble>     <workflow>

What is in final_fit? 

collect_metrics(final_fit)
#> # A tibble: 4 × 5
#>   .metric        .estimator .eval_time .estimate .config             
#>   <chr>          <chr>           <dbl>     <dbl> <chr>               
#> 1 brier_survival standard           30     0.217 Preprocessor1_Model1
#> 2 brier_survival standard           60     0.225 Preprocessor1_Model1
#> 3 brier_survival standard           90     0.160 Preprocessor1_Model1
#> 4 brier_survival standard          120     0.108 Preprocessor1_Model1

These are metrics computed with the test set

What is in final_fit? 

extract_workflow(final_fit)
#> ══ Workflow [trained] ════════════════════════════════════════════════
#> Preprocessor: Formula
#> Model: rand_forest()
#> 
#> ── Preprocessor ──────────────────────────────────────────────────────
#> event_time ~ .
#> 
#> ── Model ─────────────────────────────────────────────────────────────
#> ---------- Oblique random survival forest
#> 
#>      Linear combinations: Accelerated Cox regression
#>           N observations: 1765
#>                 N events: 1116
#>                  N trees: 1000
#>       N predictors total: 18
#>    N predictors per node: 6
#>  Average leaves per tree: 142.739
#> Min observations in leaf: 5
#>       Min events in leaf: 1
#>           OOB stat value: 0.63
#>            OOB stat type: Harrell's C-index
#>      Variable importance: anova
#> 
#> -----------------------------------------

Use this for prediction on new data, like for deploying

The whole game